This paper proposes the Discretized Integrated Gradients (DIG) method, which effectively applies the Integrated Gradients(IG) method to the word embedding space.

Integrated Gradient (IG) measures the importance of features by using the average of model gradients at interpolation points along a straight path in the input space.

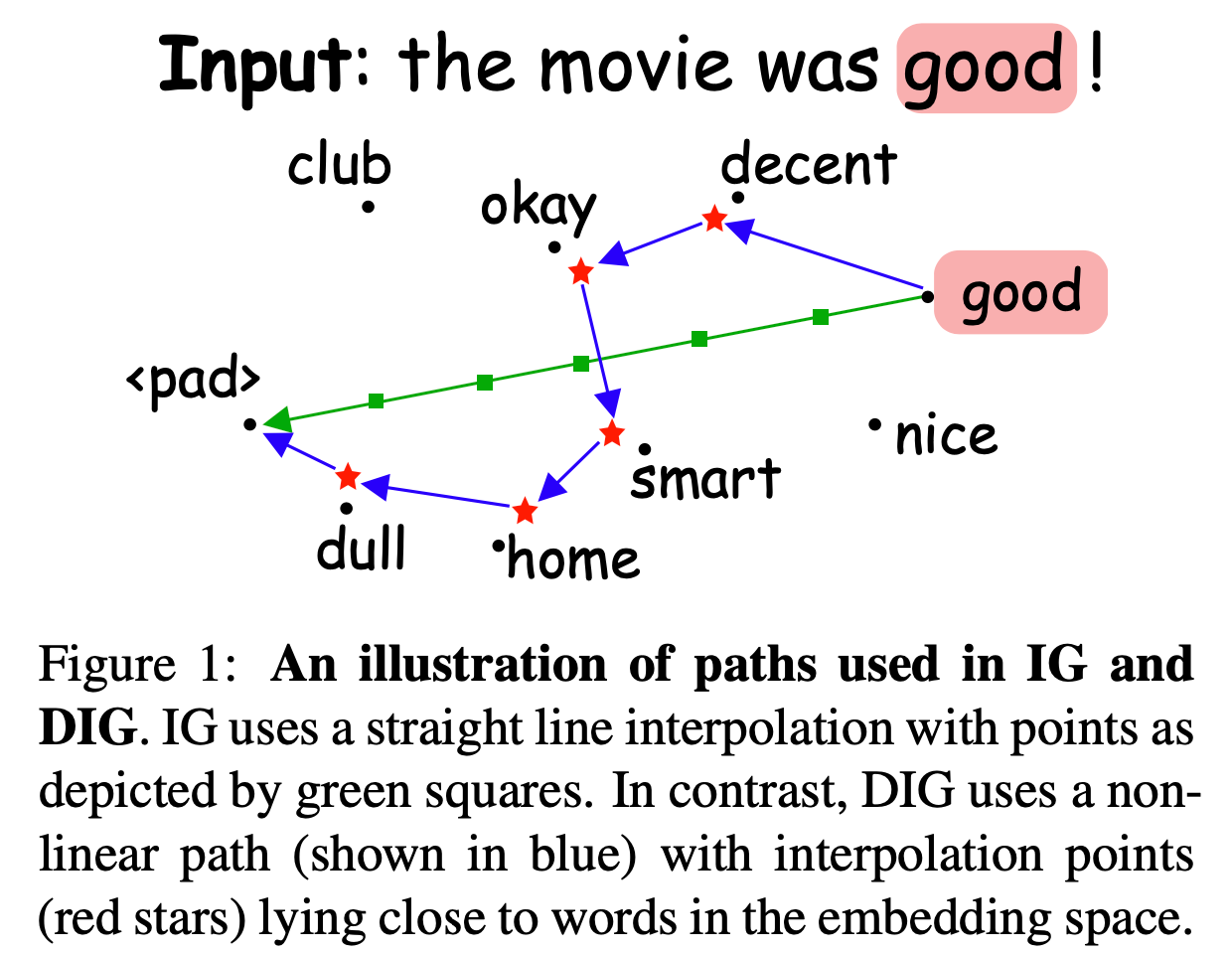
However, in the word embedding space, due to its discrete nature, interpolation points may not accurately represent textual data. In particular cases, interpolation points could be outliers.

The figure below shows that IG uses interpolation points (in green) along a straight path. In contrast, DIG uses interpolation points (red stars) on a non-linear path, which are closer to the actual word embeddings in the word embedding space.

The definition of DIG is as follows:

$$ \text{DIG}_{i}(x) = \int^{ x_i }_{ x^{k}_{i} } = x{'}_{i}\frac{\partial F(x^k)}{\partial x_i} dx^k_i, $$

where $x^k_i$ refers to the $i$-th dimension of the $k$-th interpolated point between input $x$ and baseline $x'$ and $F$ is a model to be explained. The constraint of interpolated points $x^k_i$ is that they should be monotonic between $x$ and $x{'}$. $\forall j, k \in \{1, \cdots, m\}, j $$ x'_i \leq x^j_i \leq x^k_i \leq x_i \text{ if } x'_i \leq x_i \\ x'_i \geq x^j_i \geq x^k_i \geq x_i \text{ otherwise} $$

Ensuring the constraint aims to apply Riemann summation to approximate the integral in the definition of DIG. It is as follows:

$$ \text{DIG}_{i}^{\text{approx}}(x) = \sum_{i=1}^{m} \frac{\partial F(x^k)}{\partial x_i} \times (x^{k+1}_{i} - x^{k}_{i}), $$

where $m$ is the total number of steps considered for the approximation.

The main contribution is the interpolation algorithm, which includes two steps.

Anchor search: Given an initial word embedding $w$, search for an anchor word embedding $a \in V$. The specific steps are as follows: First, find the top-K nearest neighbor for the initial word embedding $w$, denoted as $KNN_{V}(w)$

Subsequently, they propose two heuristic strategies for selecting the anchor words from $KNN_{V}(w)$, namely GREEDY and MAXCOUNT. GREEDY selects the anchor word $a$ that is closest to its corresponding monotonic embedding. MAXCOUNT selects the word from $KNN(w)$ that has the highest count of monotonic dimensions as the anchor word.

Monotonize: Given an anchor word $a$, this step modified the non-monotonic dimension of $a$ such that it becomes monotonic w.r.t. $w$ and $w'$. The monotonic dimension of $a$ is defined as follows:

$$ M_{a} = \{j|w'_{j} \leq a_j \leq w_j, j \in \{1, \cdots, D\}\} \cup \{j|w'_{j} \geq a_j \geq w_j, j \in \{1, \cdots, D\}\}, $$

where $D$ is the word embedding dimension. The non-monotonic dimension $\overline{M_a}$ is the set complement of the monotonic dimension. That is, $\overline{M_a} = \{1, \cdots, D\} - M_a$, where the minus sign denotes the set difference operation.

Denote the final monotonic embedding as $c$, then the monotonic operation is as follows:

$$ c[M_a] \leftarrow a[M_a], \\ c[\overline{M_a}] \leftarrow w[\overline{M_a}] - \frac{1}{m}(w[\overline{M_a}] - w'[\overline{M_a}] ) $$

Finally, $c$ is an interpolated point and also serves as $w$ for the next iteration. The process continues for $m$ steps.

Code

The code implementation aligns with the algorithm presented in this paper. The code is well-structured and easy to follow. Based on my review of the code, I have reconstructed the pseudocode as follows:

Assumping that text is $W = {w_1, w_2, ..., w_n}$, the corresponding embedding is $E_W \in \mathbb{R}^{n \times d}$. The raw attribution, denoted as $A \in \mathbb{R}^{n \times d}$, represents the importance of each dimension in the embedding. When evaluating the performance of explantions, they use the following formula to compute the importance score $A_w$ for each word.

$$ \begin{aligned} A_{i} &= \sum_{j=1}^{d} A_{i, j} \\ A_{w} &= \frac{A_{i}}{\Vert A_i\Vert_{F}} \end{aligned} $$

When generating the perturbed output, they remove the top-k important features while considering the sign of the attributions. In other words, postive attributions are deemed more important than negative ones.

References

EMNLP 2021 Discretized Integrated Gradients for Explaining Language Models