In machine learning, most problems are classified as Classification or Regression. However, this categorization is not always suitable for real-world problems. In some tasks, the classes are imbalanced but exhibit some weak order. In these cases, the loss functions for Classification and Regression do not perform well. This blog will apply the less commonly used margin ranking loss to address this issue.
Here is an example from the UCI Wine Quality Dataset from Cortez et al. Suppose we are a wine supplier and we find that a high review in some wine magazines increases the demand for a particular wine. Therefore, we want to predict the review score based on some measurable features of the wine. This way, we can increase the stock of the corresponding wine in advance, before the demand rises.
Assume the scores range is from 0 to 5, and this distribution is as follows:
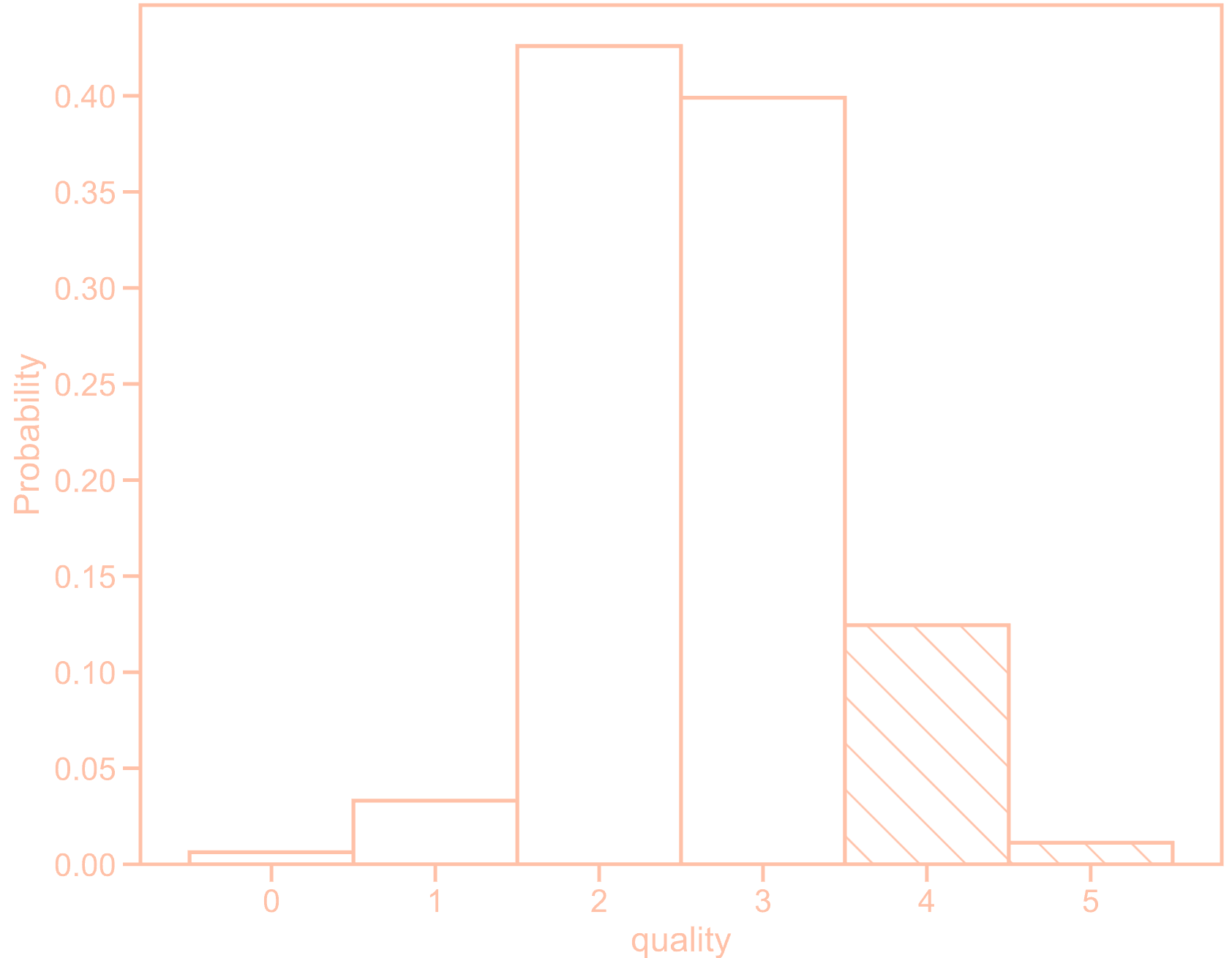Only wines with scores between 4 and 5 experience an increase in sales. Therefore, distinguishing between 3 and 4 is more important than distinguishing between 0 and 1 or 1 and 2. To predict wine scores, we can model the problem as follows:
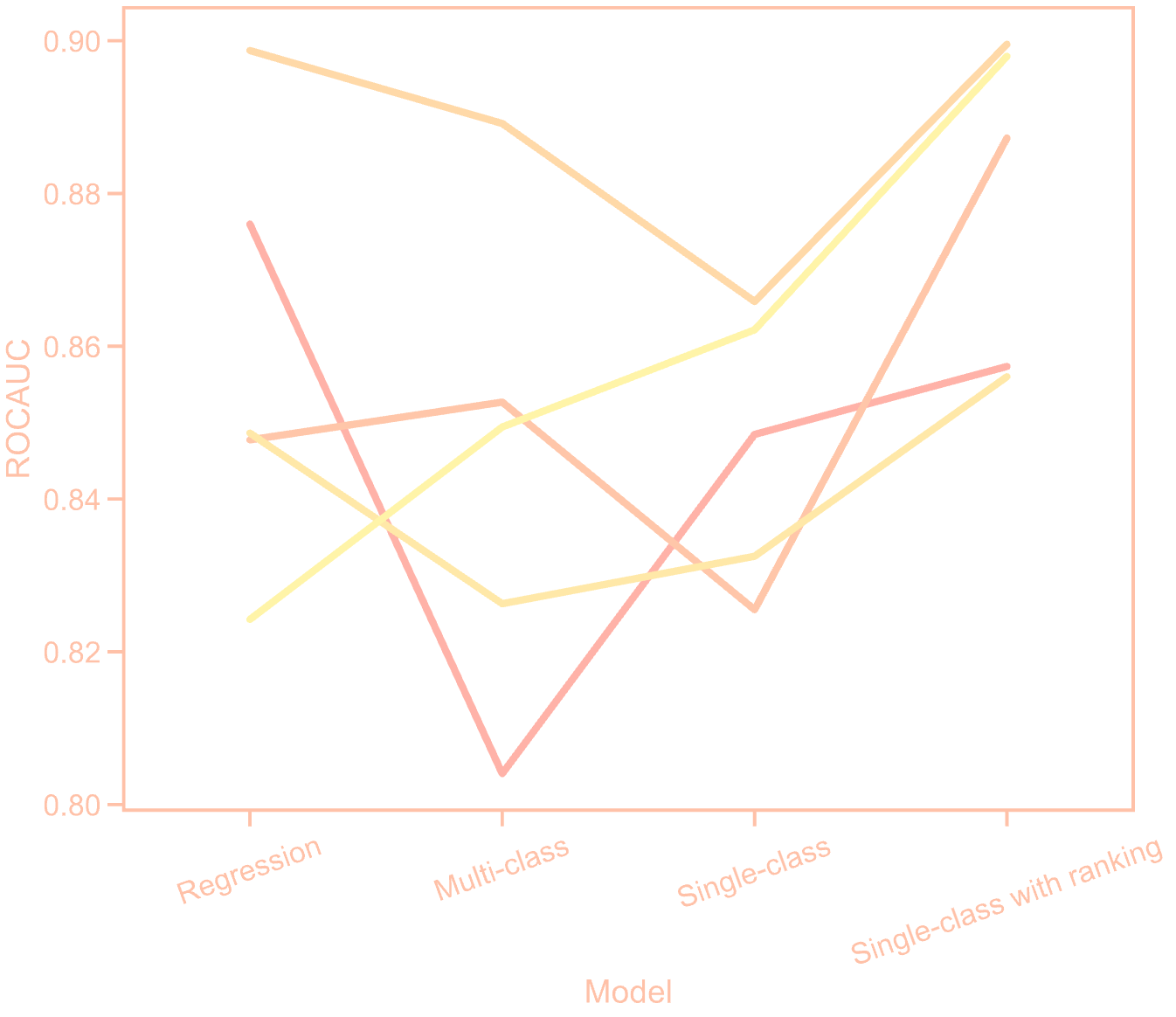
Regression. This approach captures the ranking information because the model directly predicts the wine scores in terms of distances. However, the quality score difference between 0 and 1 is considered equally important as the difference between 4 and 5. In practice, the latter is more significant, while the former can be approximately disregarded.
Multi-class. This approach treats quality scores as categorical labels, completely losing the ranking information.
Single-class. This approach frames the problem as a binary classification task, predicting whether the score exceeds 4. Although it implicitly retains some ranking information due to the two categories, it still loses a substantial amount of the ranking information between other scores.
Single-class with ranking. This method builds on Single-class by incorporating margin ranking loss to capture ranking information.
The performance comparison between different methods is shown below, with each line representing one of the five folds in cross-validation:
Implementation of Ranking loss
Margin Ranking Loss is one of the loss functions in pytorch. Its definition is as follows:
$$ \text{loss}(x_1, x_2, y) = \max(0, - y * (x_1 - x_2) + \text{margin}) $$If $y = 1$, $x_1 > x_2$, and -1 otherwise.
For the margin, there are the following cases:
- If margin = 0, the loss will be zero if x_1 and x1 in the right order.
- If margin < 0, the loss will be more forgiving, as it shifts some of the positive pair losses to zero.
- If margin > 0, the loss will be more stringent, as it changes some of the loss that are zero to positive losses.