What is Gumbel-softmax?
Gumbel-softmax is an efficient tool to sample from a categorical distribution.
Let $z$ be a categorical variable with class probabilities $\pi_1$, $\pi_2$, $\cdots$, $\pi_k$.
Before introducing the Gumbel softmax, we first present the Gumbel-Max trick. The Gumbel-Max trick is used to sample $z$ from a categorical distribution with class probabilities $\pi$:
$$ z = \text{one\_hot}(\argmax_{i}\left[g_i + log \pi_i\right]) $$where $g_1$, $\cdots$, $g_k$ are i.i.d samples drawn from Gumbel(0, 1). The Gumbel(0, 1) distribution can be sampled by drawing $u \sim \text{Uniform}(0, 1)$ and computing $g = - \log (- \log (u))$.
However, due to the use of argmax, the Gumbel-Max trick is not-differentiable operation.
To solve this issue, the softmax function is used as a continuous, differentiable approximation to the argmax function:
$$ y_i = \frac{\exp((\log(\pi_i) + g_i)/\tau)}{\sum_{j=1}^{k} \exp((\log(\pi_j) + g_j)/\tau)} \quad \text { for } i=1, \ldots, k $$Let $y = [y_1, y_2, \cdots, y_k]$.
The following figure presents the impact of $\tau$ for expectation and sample.
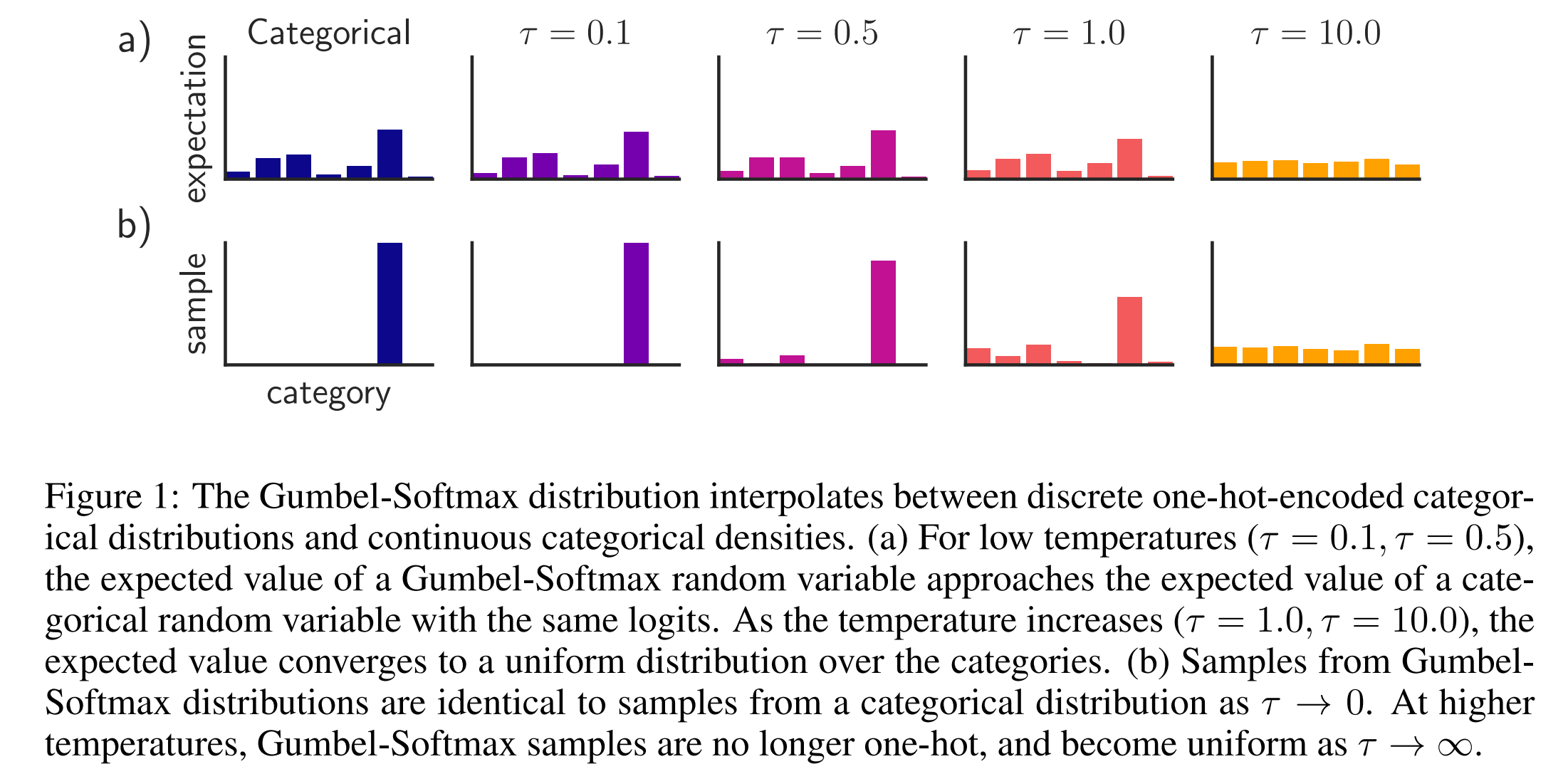
$\tau$ is an important parameter. In practice, they usually use an annealing schedule to gradually reduce the temperature during training.
Straight-through Gumbel-softmax Estimator. Although the relaxed continuous one-hot vectors are differentiable, in some scenarios where sampling of random variables is required, the discretized $y$ is non-differentiable. In these scenarios, during the backpropagation process, the gradient of continuous variable y is used to approximate the gradient of the discrete variable $z$, that is, $\nabla_{\theta}z \approx \nabla_{\theta}y$.
In the PyTorch implementation, it appears as follows:
ret = y_hard - y_soft.detach() + y_soft
In the above code snippet, during the backward pass, neither y_hard nor y_soft.detach() has gradients, while the gradients are provided by y_soft. During the forward pass, the output value of this line code equals y_hard.
We also conducted several experiments using gumbel softmax to generate images within the VAE or to generate random variables. Here is the link to the experimental code.
Relation with the Reparamaterization Trick
The reparameterization trick is employed to sample from continuous distributions.
$$ z \sim \mathcal{N}(\mu, \sigma) \rightarrow z = \mu + \sigma \epsilon \text{ where} \epsilon \sim \mathcal{N}(0, 1). $$Gumbel-Softmax is utilized to sample from categorical distribution.
$$ z \sim \left[\pi_1, \pi_2, \pi_3, \cdot, \pi_k \right] \rightarrow z = \text{softmax}(\frac{(\log(\pi_i) + g_i)}{\tau}), $$where $g = - \log (- \log (u))$ and $u \sim \text{Uniform}(0, 1)$.
References
-
Jang, E., Gu, S., & Poole, B. (2016, November). Categorical Reparameterization with Gumbel-Softmax. In International Conference on Learning Representations.
-
https://neptune.ai/blog/gumbel-softmax-loss-function-guide-how-to-implement-it-in-pytorch