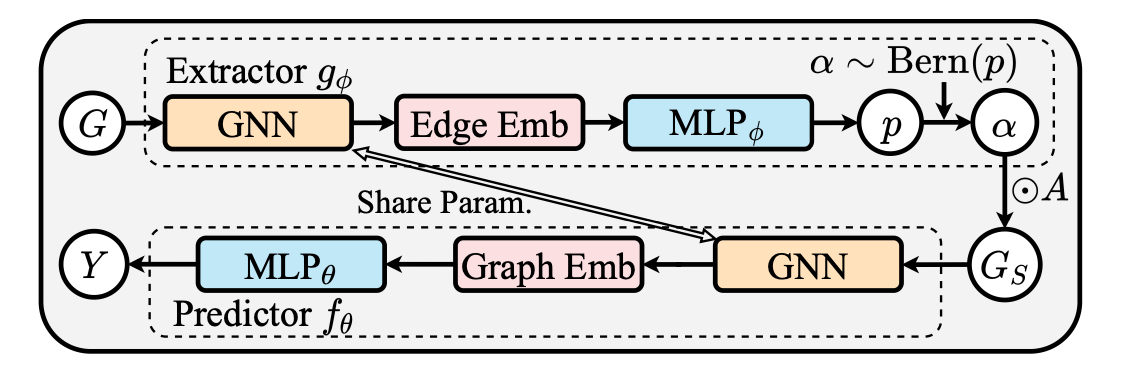
This paper introduces GSAT methods for generating explanations in graph learning. GSAT is composed of the following parts:
$G = (A, X)$ $A$ is the adjacency matrix and $X$ is the node attributes. Let $V$ and $E$ denote the node set and the edge set.
Firstly, the extractor $g_{\phi}$ encodes the input graph $G$ via a GNN into a set of node representations $(h_u | u \in X)$. For any two nodes $v$ and $u$, an MLP layer maps the concatenation of their node representations to the probability $p_{u, v} \in [0, 1]$ of an edge existing between that corresponding pair of nodes.
Secondly, stochastic attention is sampled from Bernoulli distributions $\alpha_{uv}\sim Bern(p_{uv})$. The adjacency matrix $A_S$ of the extracted graph is given by $A_S = \alpha \cdot A$, where $\alpha$ is a matrix with entries $\alpha_{uv} \in \{0, 1\}$ for $(u, v) \in E$.
Thirdly, constrain $p$ through the KL divergence between the distribution of $p$ and the Bernoulli distribution $\text{Bern}(r)$, where r is a hyperparameter.
References
Miao, S., Liu, M., & Li, P. (2022, June). Interpretable and generalizable graph learning via stochastic attention mechanism. In International Conference on Machine Learning (pp. 15524-15543). PMLR.