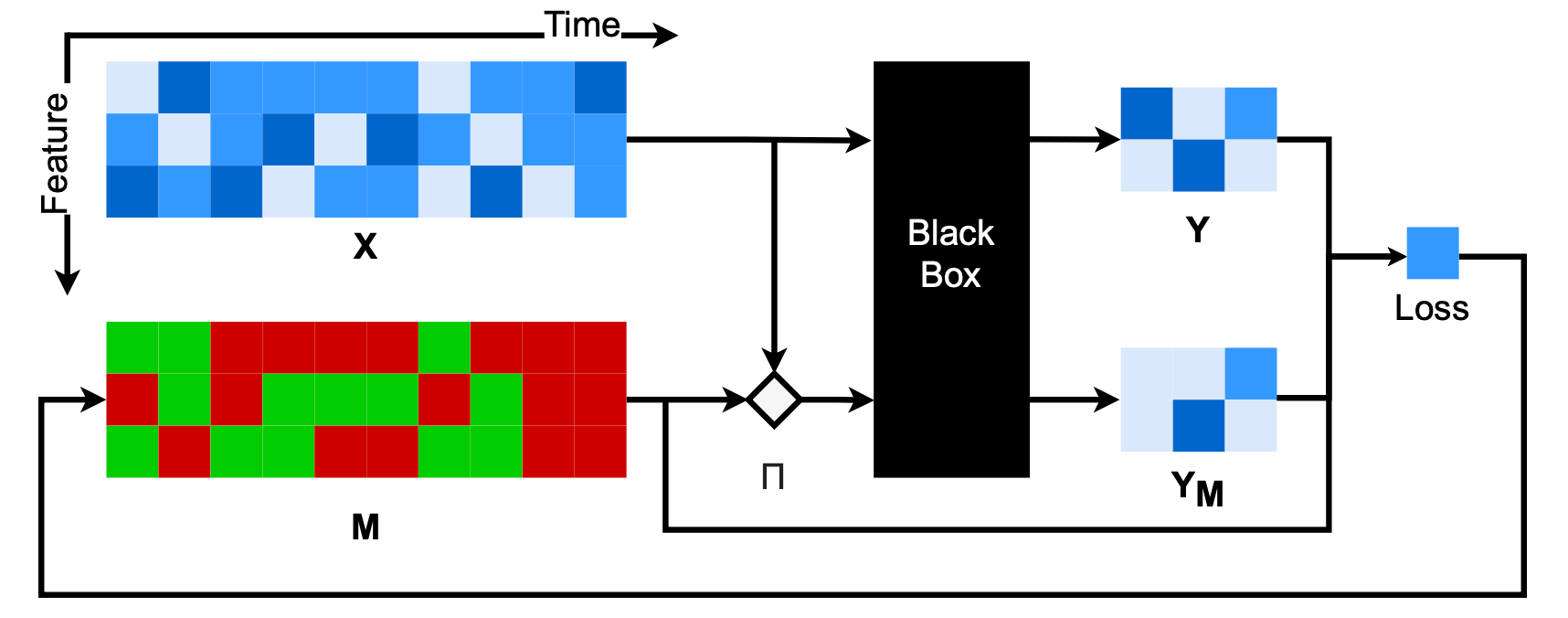
This paper is among the earliest works to learn a mask to measure the importance of each feature. Assuming a mask $M$, where $M_{t,i} \in [0, 1] $. When $M_{t, i} = 0$, this feature is irrelevant for black-box prediction. Conversely, when $M_{t, i}=1$, this feature is important for black-box prediction.
The input $x$ is perturbed based on $M_{t, i}$. A simple perturbation method is as follows:
where $b_{t,i}$ is usually generated based on the data distribution.
The objective function aims to minimize the cross-entropy between the unperturbed and the perturbed predictions.
$$ L(M) = \sum_{c=1}^{C} f(x) \log f(x') $$References
Crabbé, J., & Van Der Schaar, M. (2021, July). Explaining time series predictions with dynamic masks. In International Conference on Machine Learning (pp. 2166-2177). PMLR.