The main contributions of this paper are twofold:(1) investigating the Out-of-Distribution (OOD) problem in counterfactual inputs, and (2) proposing a Parallel Local Search (PLS) method for generating explanations.

Out-of-Distribution Problem

The possible causes of the OOD problem in FI explanations are shown in the following figure. alt text Even on in-distribution data, neural networks are sensitive to random parameter initialization, data ordering, and hyperparameters. Therefore, neural networks are also influenced by these factors when processing OOD data.

To address the OOD problem, they propose Counterfactual Training to align the training and testing distributions. The core step of Counterfactual Training involves training a neural network using random explanations that remove most input tokens.

Evaluating OOD performance for different Replace functions

Robustness is measured by model accuracy, and the evaluation steps are as follows:

  • Evaluate five different Replace functions on the same explanation.
  • Compute the accuracy change for each removal proportion of features.
  • For each removal proportion of features, the smaller the accuracy change, the better the Replace function performs in addressing the OOD problem.

Result

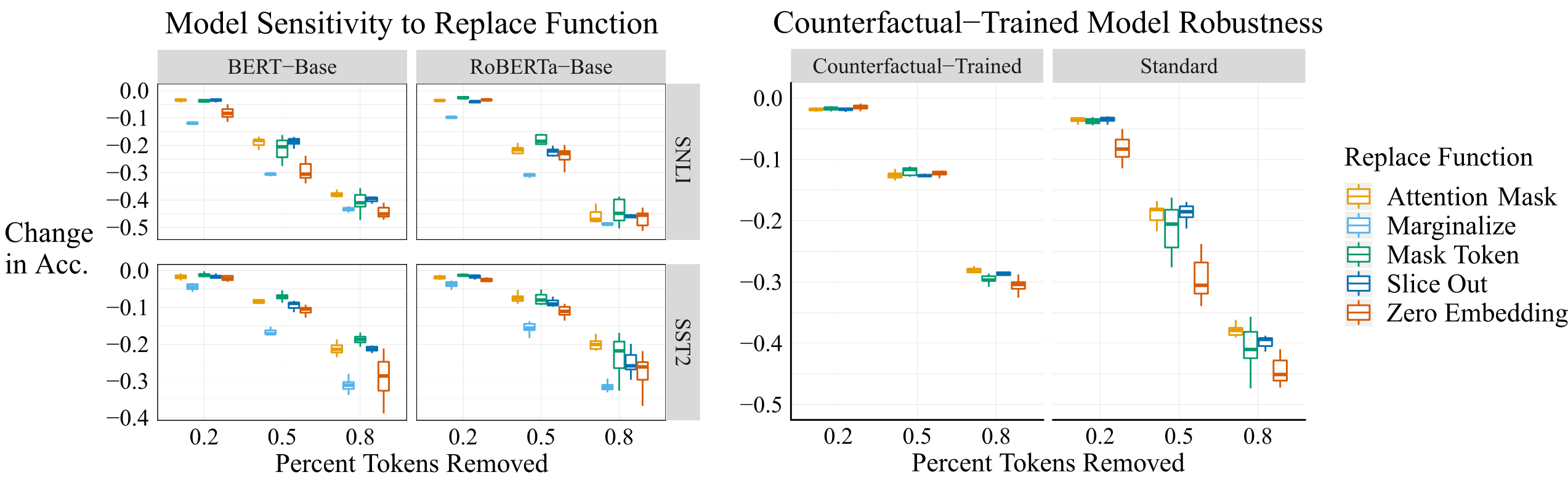alt text (1) The Attention Mask and Mask Token functions are the two most effective methods. (2) Counterfactual training mitigates the OOD problem for counterfactual inputs.

Search methods for explanation

They propose a novel search method, Parallel Local Search (PLS), to explain feature importance.

While running other search methods, I encountered some minor issues. Therefore, I referred to both the source code and the corresponding content in the paper. Based on my understanding, the search methods aim to explore all possible binary explanation vectors $e \in {0, 1}^d$ to identify the optimal explanation under the following two metrics:

$$ \text{Suff}(f, x, e) = f(x)_{\hat{y}} - f(\text{Replace}(x, e))_{\hat{y}} $$$$ \text{Comp}(f, x, e) = f(x)_{\hat{y}} - f(\text{Replace}(x, e))_{\hat{y}} $$

For instance, exhaustive search evaluates all possible binary explanation vectors to find the most suitable one.

Code: https://github.com/peterbhase/ExplanationSearch

References

The out-of-distribution problem in explainability and search methods for feature importance explanations NeurIPS 2021