The definition of Binary Cross-Entropy is given by:
$$ L(y, p) = - [y\log(p)+ (1-y)\log(1-p)] $$where $y \in [0, 1]$ represents the soft target (i.e., a probability rather than a hard label), and $p \in (0, 1)$ is the predicted probability.
The gradient of $L(y,p)$ with respect to $p$ is:
$$ \frac{\partial L}{\partial p} = \frac{p-y}{(1-p)p} $$Based on the gradient, we observe that:
- In the interval $[0, y)$, $L$ decrease monotonically.
- In the interval $(y, 1]$, $L$ will increase monotonically.
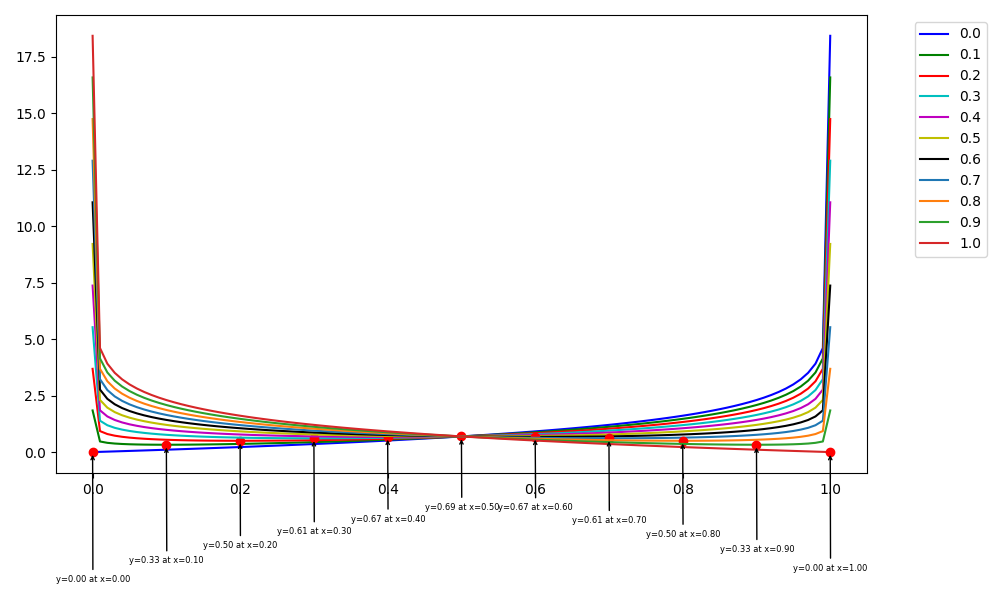
Therefore, $L$ attains its minimum at $p=y$. The minimum value of $L$ is $- [y\log(y)+ (1-y)\log(1-y)]$, which corresponds to the information entropy of the Bernoulli distribution with probability $y$.
In particular, when y = 1 or 0, the minimum of $L$ is zero, which is often the case in classification tasks.
I plot the binary cross-entropy loss curves for different values of $y \in [0.0, 0.1, 0.2, ..., 1.0]$. The figure below shows the results, where the red point on each curve indicates the minimum of the corresponding loss function.